
3D Fun

 |
 |
 |

3D Printing and Hardcopy - Introduction
3D prints can be made by at least two different methods. In one method, known as an anaglyph, a pair of views of a scene is printed with two colors, usually red for the left eye and blue for the right eye (red and green are also sometimes used). One then uses a matching pair of color filters, red for the left and blue for the right eye, to view the anaglyph in stereo. Simple 3D glasses for viewing anaglyphs can be obtained from several companies, e.g., David Burder's company, 3D Images, Ltd. Books of anaglyphs, such as Scaly and Slimy In 3-D by David Burder can be obtained from Amazon for example.In another method, both 3D and animation hardcopy can be produced by printing on lenticular screens. A lenticular screen is a sheet, usually made of plastic, of very small half-cylindrical lenses spaced very close together. From 75 to 250 lenticules per inch are typically used, with lithography being the method of printing used at the coarse end of the range, and photography being the only method possible at the fine end. When 250 or more lenticules per inch are used, the individual lenticules are essentially invisible to the unaided eye. One of the world's best manufacturers of lenticular material is Ken Conley's company Micro Lens Technology, Inc. (704-847-9234). When such a screen has its rear surface coated with a photosensitive emulsion, and is exposed to light representing different views of a 3D image or different scenes from an animation, from several different directions and developed, a 3D or animation hardcopy print results. When the 3D print is observed with the axes of the lenticules vertical, each eye sees a different view from the original set exposed onto the screen. If these views were constructed as different views of a set of objects at various distances, then the viewer experiences parallax in looking at the print. A set of images with two views will give a stereoscopic effect, but more than two views will result in an autostereoscopic effect where it is possible to look around objects on the print. For an animation, where different scenes are exposed onto the lenticular screen, the viewer must orient the axes of the lenticules horizontally and rotate the print slightly about a horizontal axis to experience the effect of changing scenes.
The method just described is sometimes known as the direct photographic process. In the indirect method one first produces a composite, or interlaced image, and then laminates it to a sheet of lenticular material. The interlaced image can be produced by photographically exposing an emulsion placed behind a recording lenticular screen, or by printing the interlaced image stripes on a sheet of opaque or transparent material with an offset press or ink jet printer. When laminating the print or transparency to the lenticular material, one has to very carefully align the interlaced image stripes with the lenticules. Because of the difficulty of this last step, the maximum pitch (number of lenticules per inch) of the lenticular material is usually limited to about 100 lenticules per inch. On the other hand the field of view of prints made with image stripes printed by an offset press, ink jet or other printer, can be quite a bit larger than those created photographically. This is due to the larger required physical size of the photographic scanning apparatus, and the larger required field-of-view of the projection lens.
In the direct photographic process, the interlaced image is automatically aligned when the light that exposes the emulsion passes through the lenticules. To create a print by a direct non-photographic approach, say by lithography, one must be sure that print head is aligned and remains aligned with the lenticules during the printing process. One approach is to use lenticular material which has its edges parallel to the axes of the lenticules, and keep the edge of the material pressed against a guide in the printer. This is known in the industry as "edge guiding". A number of trial prints is usually necessary before the central interlaced stripe winds up directly beneath the center of corresponding lenticule. For both the direct and indirect non-photographic processes, it is important to carefully compute the pitch of the image stripes in the interlaced image that the computer sends to the printer. First one has to decide upon the number of views that will go into the composite image, the pitch of the lenticular material, and the actual size of the print. If four views are used, say, then there will be approximately four stipes per lenticule. Next one must calculate the precise pitch from a formula. The exact relationship depends on the viewing distance from the print, which in turn has an empirical dependence on the size of the print. In another approach to direct non-photographic printing, the printing apparatus senses the precise location of the print head relative to the lenticules, and compensates for any errors. A device called a lenticular linear encoder, or LLE (U.S. Patent 6060720) recently invented by Donald Gudehus should in the future make this approach feasible.
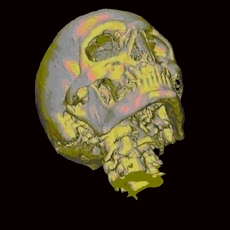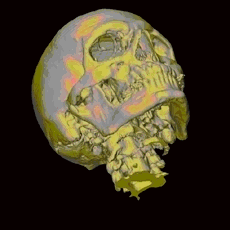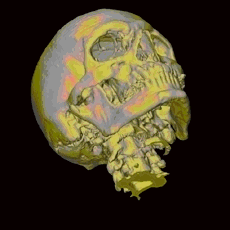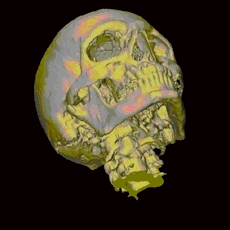
The images at the top of this page demonstrate the changing views and scenes that one can experience with 3D and animation lenticular hardcopy prints. In the first image, individual slides of Saturn and its satellites were scanned and combined with Photoshop to produce seven views from different directions. The set was arranged so that there is zero parallax for the satellite Rhea. Dione, the satellite with the largest angular size, has the largest parallax. Titan, Saturn's largest satellite, is in the upper right corner and has a parallax of the opposite sign and somewhat smaller in magnitude. In the second image above, a photo of Papilio g. glaucus (sometimes shortened to Papilio glaucus), the Tiger Swallowtail, and a flower were combined in Photoshop with the wings of the butterfly gradually foreshortened over six scenes to give the illusion of the wings opening and closing. The last image above was created from an MRI scan of a skull which was then segmented and colorized. In this case a plane passing through the middle of the skull has been adjusted to have zero parallax. This is known as the key subject plane. The first two images were created by Donald Gudehus and the last one by the award winning photojournalist and artist, Alexander Tsiaras. Alexander Tsiaras is well known for his "Body Voyage" CD-ROM, a three-dimensional tour of a real human body, and his "Anatomical Travelogue", a unique series of articles, films, multimedia projects, and books about the human body. To see more animated images, click here.
3D Photography and Software
In order to create a set of images representing different views of a 3D image, one could take a series of photographs from different positions and directions with a single camera. Although it is possible to simply shift your position while holding the camera in your hand, it is not easy to control the camera's direction and position during this process. Usually, a camera track, supported by a tripod, is used for this purpose. A graduated scale on the track allows for precise positioning, and the horizontal slide mechanism keeps the camera pointed in the same direction between shots. While it may seem intuitive to keep the subject centered in the camera's field of view from one exposure to the next instead of always keeping the camera pointed in the same direction, such an approach will produce a keystoning effect, where the magnification of the subject, from left to right, varies from exposure to exposure. Although it is not possible to eliminate magnification variations from one frame to the next in the exposure sequence, the effect is minimized by keeping the camera always pointed in a fixed direction. Tracks can be home made or bought from a commercial manufacturer. The former 3D Image Technology, Inc. (3DIT or Image Tech) used to sell an excellent track, but the company is no longer in business. The location of the camera on a track can be easily calculated with the aid the free computer program, CompuTrack, written by Donald Gudehus for the Macintosh (68k and Power PC). Just input two of the three distances (foreground, key subject, and background), the film format, the lens focal length, and the print width, and the program gives the increment in millimeters by which to advance the camera between each of seven shots. If instead of taking a sequence of photos of a scene, you are rendering a scene with a 3D modeling program, the CompuTrack program can help by calculating the angle in degrees by which to rotate the key subject. Some current 3D modeling programs are Alias Wavefront's Maya, AutoDesSys's form*Z, Eovia Corp.'s Ray Dream Studio, Infini-D, and Carrara, Innoventive Software's FrameForge 3D Studio, Maxon Computer's Cinema 4D R8, NewTek, Inc.'s LightWave 3D, and Strata's Strata 3D CX. An important requirement in shifting the camera between one position and the next, or in rotating the key subject in a 3D modeling program, is the human brain's limit for fusing together two views containing parallax shifts. Experiments show that a person's upper limit for this is about one degree. The CompuTrack program takes this limit into consideration, and also applies a condition that the parallax of the background subject should be twice that of the foreground subject, when referenced to the key subject. These empirical algorithms give excellent results in most cases.The photographic technique described above is acceptable for scenes which do not evolve in time. For time evolving scenes, one will need to use either a camera with several lenses, or a set of single lens cameras which can be triggered simultaneously. Consumer cameras with three lenses were long sold by the now defunct 3D Image Technology, Inc. and 3D Imaging Systems, Inc, the company that until about 2002, continued its operations. These cameras were very popular since little experience was necessary to take good 3D photographs, and the processing and printing were handled by the company. Consumer cameras with four lenses were manufactured by Nimslo in the 1980s but that company also no longer exists. Professional cameras with five lenses were available from 3D Image Technology, Inc. Because in a multilens camera, the horizontal spacing between lenses is fixed, there is no need to use CompuTrack to calculate the horizontal increment. CompuTrack can however be used to calculate one of the three distances, foreground, key subject, and background, given the other two.
There are some exceptional situations where a multilens camera or a track will not serve its intended purpose. For example, with a cityscape or mountain scene, the key subject distances could be several kilometers, and the resulting horizontal spacing between exposures would then be many tens of meters. For the aurora, the key subject distance is about 100 kilometers, and the subject also evolves rapidly with time. People have handled these cases by photographing from an aircraft or stationing several cameras along a path with attending photographers in radio communication.
If you are not using a multilens consumer or professional camera where the printing is handled by the camera compnay, then after you have either photographed or rendered your subject in a series of frames, you will need to be sure that each frame aligns with the others in the key subject area. You may also need to do some cropping and/or filling to ensure that each frame has the same number of pixels. The alignment can be done manually with Photoshop or automatically with specialized software. It is often very useful to see a time-repeating sequence of the images to be sure that the alignment is perfect and that there are no unexpected artifacts in one or more of the frames. If you have an SGI computer, the program "movie" will do this for you provided that the images are in SGI format. If you are using a Power Macintosh and have PICT images, the free program MacMovie, by Donald Gudehus will also display a movie-like sequence as well as providing some additional features.
People sometimes wonder if it is possible to convert a 2D image into a 3D image. Provided that one can identify various subjects within the 2D picture, associate them with their relative distances, and then shift them by varying amounts in order to create a sequence of images with gradually increasing parallax, it can be done. The displacements, in units of pixels, can be done manually or by means of software written for this purpose. As mentioned above, the maximum induced shifts should not exceed a parallax of about one degree as viewed on the print.
The 3D Print
If you have access to a 3D digital printer which uses the photographic process (the world's first digital 3D printer was invented at 3DIT), you can just submit your files for printing. If on the other hand you wish to or need to use a non-photographic process, you will have to interlace the images. This needs to be carried out by a computer program which merges together the various individual files into one interlaced file. Since the output file is the same width and height (in terms of pixels) as each of the individual files, some information is lost in this process, but only in the horizontal direction. The free programs interlace which runs on Linux with Intel processors, and Interlace which runs on the Macintosh can carry out this step. When interlacing the frames, the stripe at the left of each group of frames represents the frame photographed with the camera at its rightmost position. If by accident, the sequence of frames is reversed, then objects in the background will seem to be in the foreground, and vice versa. The resulting 3D image is then said to be pseudoscopic. The resolution of the interlaced file, measured in pixels per inch say, has to be precisely calculated as a function of the pitch of the lenticular screen, the number of frames, and the viewing distance (which is an empirical function of the print width). Since the resolution affects the print size, the desired print size should be decided upon before interlacing and the files expanded or contracted as necessary. Therefore, before using the interlace programs referred to above, you should run either of the free programs 3d_resolution which runs on Linux with Intel processors, or Mac 3D Resolution which runs on the Macintosh. Simply input the desired print width, the exact pitch (see below) of the lenticular screen, the field of view of the lenticules, and the number of frames, and the program will calculate the width in pixels that your files should be expanded or contracted to, and the required resolution of the final interlaced file. If you use Photoshop to expand or contract your files, go to the "Image" menu, select "Image Size...", be sure "Constrain Proportions" and "Resample Image" are checked, enter the new width in pixels, and click "OK". Don't be concerned about the width in inches or the resolution at this stage. After interlacing, but before printing, you should set the resolution of your interlaced file to the required value with the "Resample Image" box unchecked.To obtain the exact pitch of your lenticular screen, you need to view a calibration chart that is placed directly in back and in contact with the lenticular screen, and with the black lines of the chart running in the same direction as the lenticules. The calibration chart is simply a set of closely spaced black lines of various pitches, close to the pitch of your lenticular sheet. For example, if the sheet you ordered is 72 lpi, the chart might have sets of closely spaced lines at pitches of 71.5, 71.6, ..., 72.4, and 72.5 lpi. For the pitches that don't match that of your screen you will see an alternating black and white pattern, but for the matching pitch the pattern will be a uniform gray. If an exact match is not apparent, try to estimate a best value by interpolating between the two pitch values that have the slowest varying patterns. However, it may be that the calibration chart is out of range for your particular lenticular screen, as evidenced by all the visible patterns varying too rapidly. In that case choose a chart with a slightly higher or lower range of pitches until a match is found. In order to obtain the most accurate value, view the patterns from several feet away. Some calibration charts are available for download here.
Built in to the 3d_resolution programs is the above mentioned empirical relationship of viewing distance to print width. If you imagine being very far away from a 3D lenticualr print, then each of your eyes sees the same set of stripes under the lenticules and so there is no 3D effect. If on the other hand you move very close to the lenticular print, then the width of the print will subtend an angle relative to each of your eyes that is greater than the intrinsic field-of-view of the lenticular screen. In this case the image will appear to suddenly shift in angle as you look from one side of the print to the other because rays from the wrong stripes under the outlying lenticules will be entering your eyes. At some critical distance, the print width subtends an angle equal to the field-of-view of the lenticules, and the desired 3D effect will be present with no unexpected image shift. Actually one can view the print slightly farther away than the critical distance with no significant detriment. In this situation the print can be rotated slightly about a vertical axis to "see around" objects in the 3D print, and obtain an autostereoscopic effect. The empirically determined relationship of optimum viewing distance as a function of print width is given by d = 5.0 + 1.34W -0.016W2, where d, the distance, and W, the width, are in inches. For a print width of 5 inches, the viewing distance comes out to be 11.3 inches. For very wide prints (over 30 or 40 inches) this formula becomes inaccurate (as do the 3d_resolution and Mac 3D Resolution programs), however an updated formula and updated programs will eventually be available.
Generally, digital artists prefer to use file formats which do not use destructive compression. In the case of interlaced images it is particularly important that no degradation of the output image occur. Thus, the preferred file formats for 3D printing are PICT, TIFF, and SGI. The Linux program, interlace, uses the TIFF format only, and the Macintosh program, Interlace, uses the PICT format only. Information on making 3D prints with an inkjet printer will be available here at some time in the future. For general information about printing on an inkjet printer, see the web page Inkjet Printer Hints.
3D Informational Links
Email: